DIY Electronics
Simple electronics as a hobby
True random number generator
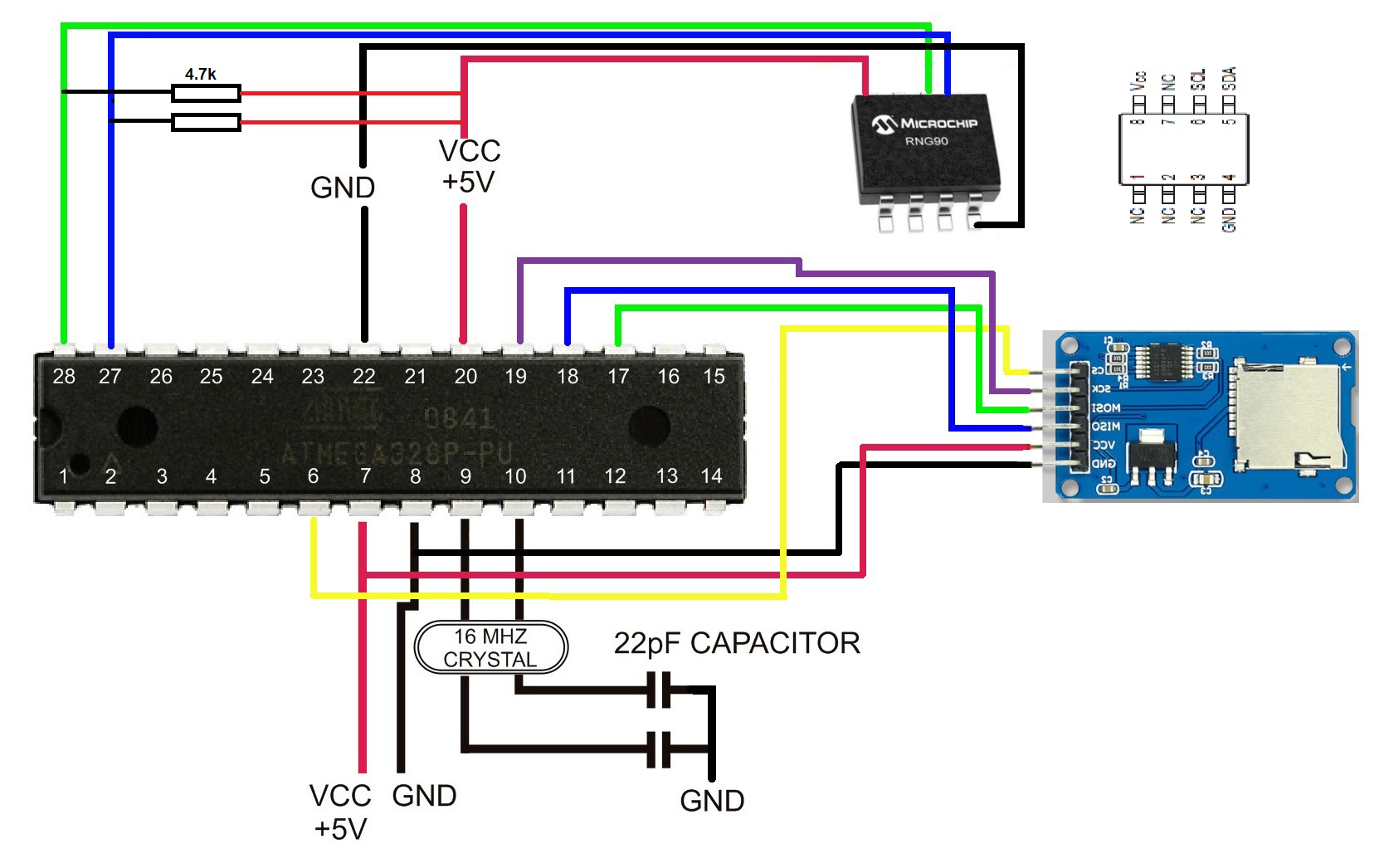 Microchip developed the RNG90 chip per NIST specifications and certified the device working with a NIST-certified laboratory. The chip uses a physical non-deterministic noise source (NRBG producing an entropy bit stream) seeding a deterministic algorithm (DRBG). It generates a 256-bit random number that has a security strength of 128 bits each time the Random command is executed.
Microchip developed the RNG90 chip per NIST specifications and certified the device working with a NIST-certified laboratory. The chip uses a physical non-deterministic noise source (NRBG producing an entropy bit stream) seeding a deterministic algorithm (DRBG). It generates a 256-bit random number that has a security strength of 128 bits each time the Random command is executed.
The Arduino code works, but is probably not the best way to generate 32 bytes of random numbers. The first execution of the random command excludes the wire.write of the i2c-address (0x40). The second run of the random command the wire.write 0x40 is included and that produces the 32 bytes output. Why? I don't know. I also discard the first byte being 35 (0x23) each time around.
>>> Arduino Uno code to read rng90 microchip <<<
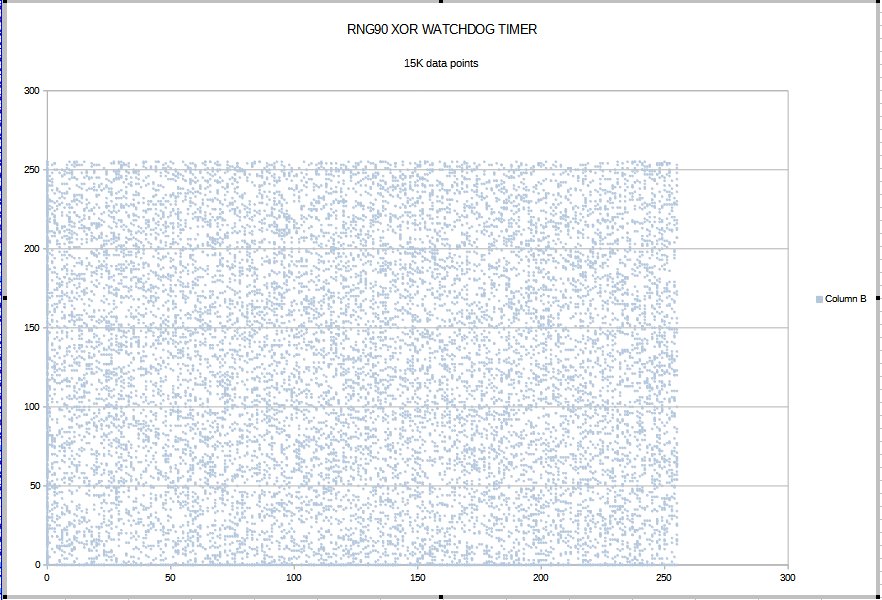 The next arduino sketch uses the same hardware setup, but the code generates random numbers using the watchdog timer interrupt and combines the output with the numbers of the rng90 applying XOR. The watchdog timer has a different oscillator (128KHz) than the other timers. It also seems to be less accurate. The timer's drift produces randomness, especially looking at the lower byte of timer TCNT1.
The next arduino sketch uses the same hardware setup, but the code generates random numbers using the watchdog timer interrupt and combines the output with the numbers of the rng90 applying XOR. The watchdog timer has a different oscillator (128KHz) than the other timers. It also seems to be less accurate. The timer's drift produces randomness, especially looking at the lower byte of timer TCNT1.
I saw the writing to file gets slower over time, because after every close datafile a new open datafile has to find the end of a large file. It works better not closing the file at all, but just flush the data after writing a line.
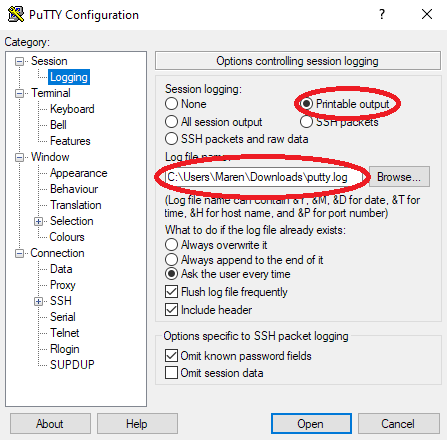
The following arduino sketch prints the output to the serial interface. With putty you can capture the output in a file. Two buttons pressed separately or together generates 4 different results: decimal, hexadecimal, binary or dice numbers.
I changed the Print.ccp (print::printNumber method) in appdata to print leading zeros for both binary and hex.
do {
char c = n % base;
n /= base;
*--str = c < 10 ? c + '0' : c + 'A' - 10;
cnt++; // added
} while(n);
// added
if (base == 2) {
while (cnt++ % 8) *--str = '0';
}
else if (base == 16) {
if (cnt++ % 2) *--str = '0';
}
 >>> Arduino Nano serial output <<<
>>> Arduino Nano serial output <<<NIST test suite
 NIST Computer Security Resource Center
NIST Computer Security Resource Center
offers a statistical test suite for the validation of Random Number Generators and Pseudo Random Number Generators for Cryptographic Applications.
Link to the software sts-2_1_2.zip
Link to the documentation pdf (including installation & usage Chapter 5)
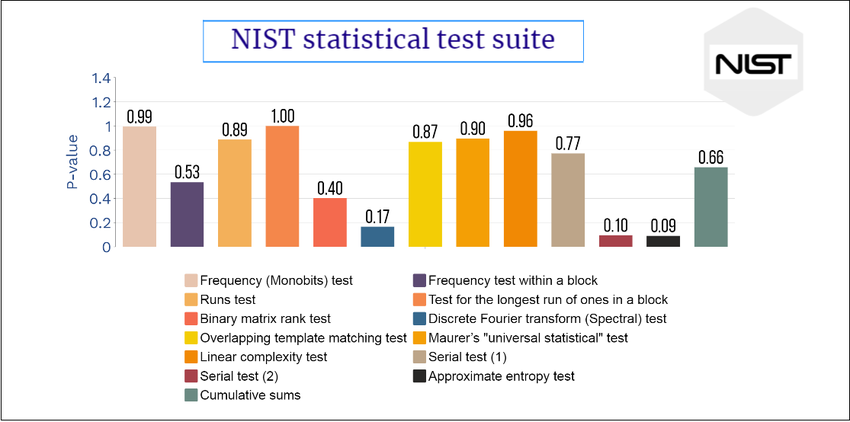
Image is just an illustration.
Next section is part of "1.1.5 Testing" of the above mentioned documentation.
Statistical hypothesis testing is a conclusion-generation procedure that has two possible outcomes, either accept H0 (the data is random) or accept Ha (the data is non-random). The following 2 by 2 table relates the true (unknown) status of the data at hand to the conclusion arrived at using the testing procedure.
| True situation | Conclusion | |
|---|---|---|
| Accept H0 | Accept Ha (reject H0) | |
| Data is random (H0 is true) | No error | Type I error |
| Data is not random (Ha is true) | Type II error | No error |
If the data is, in truth, random, then a conclusion to reject the null hypothesis (i.e., conclude that the data is non-random) will occur a small percentage of the time. This conclusion is called a Type I error. If the data is, in truth, non-random, then a conclusion to accept the null hypothesis (i.e., conclude that the data is actually random) is called a Type II error. The conclusions to accept H0 when the data is really random, and to reject H0 when the data is non-random, are correct.
The probability of a Type I error is often called the level of significance of the test. This probability can be set prior to a test and is denoted as α. For the test, α is the probability that the test will indicate that the sequence is not random when it really is random. That is, a sequence appears to have non-random properties even when a “good” generator produced the sequence. Common values of α in cryptography are about 0.01.
The probability of a Type II error is denoted as β. For the test, β is the probability that the test will indicate that the sequence is random when it is not; that is, a “bad” generator produced a sequence that appears to have random properties. Unlike α, β is not a fixed value. β can take on many different values because there are an infinite number of ways that a data stream can be non-random, and each different way yields a different β. The calculation of the Type II error β is more difficult than the calculation of α because of the many possible types of non-randomness.
One of the primary goals of the following tests is to minimize the probability of a Type II error, i.e., to minimize the probability of accepting a sequence being produced by a generator as good when the generator was actually bad. The probabilities α and β are related to each other and to the size n of the tested sequence in such a way that if two of them are specified, the third value is automatically determined. Practitioners usually select a sample size n and a value for α (the probability of a Type I error – the level of significance). Then a critical point for a given statistic is selected that will produce the smallest β (the probability of a Type II error). That is, a suitable sample size is selected along with an acceptable probability of deciding that a bad generator has produced the sequence when it really is random. Then the cutoff point for acceptability is chosen such that the probability of falsely accepting a sequence as random has the smallest possible value.
Each test is based on a calculated test statistic value, which is a function of the data. If the test statistic value is S and the critical value is t, then the Type I error probability is P(S > t || Ho is true) = P(reject Ho | H0 is true), and the Type II error probability is P(S ≤ t || H0 is false) = P(accept H0 | H0 is false). The test statistic is used to calculate a P-value that summarizes the strength of the evidence against the null hypothesis. For these tests, each P-value is the probability that a perfect random number generator would have produced a sequence less random than the sequence that was tested, given the kind of non-randomness assessed by the test. If a P-value for a test is determined to be equal to 1, then the sequence appears to have perfect randomness. A P-value of zero indicates that the sequence appears to be completely non-random. A significance level (α) can be chosen for the tests. If P-value ≥α, then the null hypothesis is accepted; i.e., the sequence appears to be random. If P-value <α, then the null hypothesis is rejected; i.e., the sequence appears to be non-random. The parameter αdenotes the probability of the Type I error. Typically, α is chosen in the range [0.001, 0.01].
The results of the test suite applied to random numbers generated by the rng90, rng90 xor-ed with watchdog timer and by a simple c-program were all successfull. In the first run 1 million bytes (8 million 0's and 1's) were used. In a second run 1 billion pseudo-random bytes were applied to see if a larger number would make a difference. The p-values were high enough to suggest randomness. Also using multiple bitstreams (10) didn't make any difference. This means that a simple pseudo random generator is as good as non-pseudo, specific rng90 microchip, according to the NIST test suite.
The pseudo-rng C-program looks like this:
srand(time(NULL));
for (int i=0; i < 1000000; i++) {
r = rand() % 256;
fprintf(fp,"%d,",r);
}
Another pseudo random source that has a high success rate on the NIST tests is this one:
dd if=/dev/urandom of=/tmp/testfile.bin bs=1k count=2500
TestU01
TestU01 is a software library, implemented in the ANSI C language, and offering a collection of utilities for the empirical statistical testing of uniform random number generators.Website simul.iro.umontreal.ca/testu01/tu01.html
To test random numbers from an external source you need a file with unsigned 4 byte integers and feed it to the library. I think that you need at least 10 million numbers to see any positive results. When creating a file using the xorshift function 1 million numbers give a positve result for just a few of all 15 tests, but 250 million numbers do much better. This is the code to import a file (my_random_numbers.txt):
#include <stdio.h>
#include "unif01.h"
#include "bbattery.h"
FILE *input_file;
unsigned long cnt=0;
unsigned int file_random(void) {
unsigned int num;
if (fscanf(input_file, "%u", &num) != 1) {
// If we reach end of file, rewind to the beginning
rewind(input_file);
fscanf(input_file, "%u", &num);
}
cnt++;
return num;
}
unif01_Gen *create_file_generator(const char *filename) {
input_file = fopen(filename, "r");
if (input_file == NULL) {
printf("Error opening file %s\n", filename);
return NULL;
}
return unif01_CreateExternGenBits("File Random Number Generator", file_random);
}
int main() {
unif01_Gen *gen = create_file_generator("my_random_numbers.txt");
if (gen == NULL) return 1;
// Run the Small Crush battery of tests
bbattery_SmallCrush(gen);
// Optionally, run more extensive test batteries:
// bbattery_Crush(gen);
// bbattery_BigCrush(gen);
// Clean up
unif01_DeleteExternGenBits(gen);
printf("numbers read: %lu\n", cnt);
fclose(input_file);
return 0;
}
To compile the file "file_rng_test.c" use
gcc -o file_rng_test file_rng_test.c -ltestu01 -lprobdist -lmylib -lm
Next run the file ./file_rng_test
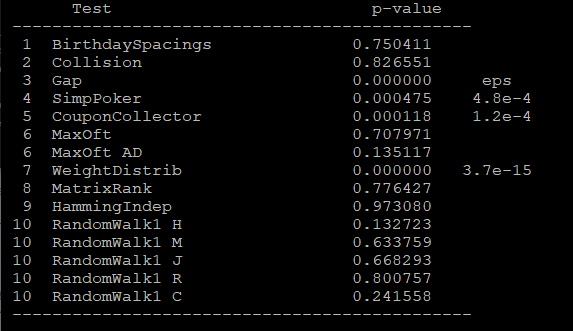
When you see "eps" in TestU01 results, it means the random number generator being tested performed very poorly on that specific test, showing strong statistical patterns or biases that a high-quality RNG shouldn't exhibit."1-eps1" in TestU01 results indicates a p-value that is extremely close to 1 (specifically, 1 minus a very small epsilon value).This suggests there might be a problem with the random number generator where it's producing patterns that are unrealistically well-distributed.
Running dd if=/dev/urandom of=/tmp/random_bits.bin bs=1k count=50000 and then converting it into a text file of integers will give the following results on the Small Crush battery of tests