DIY Electronics
Simple electronics as a hobby
Explanation of Diffie-Hellman key exchange
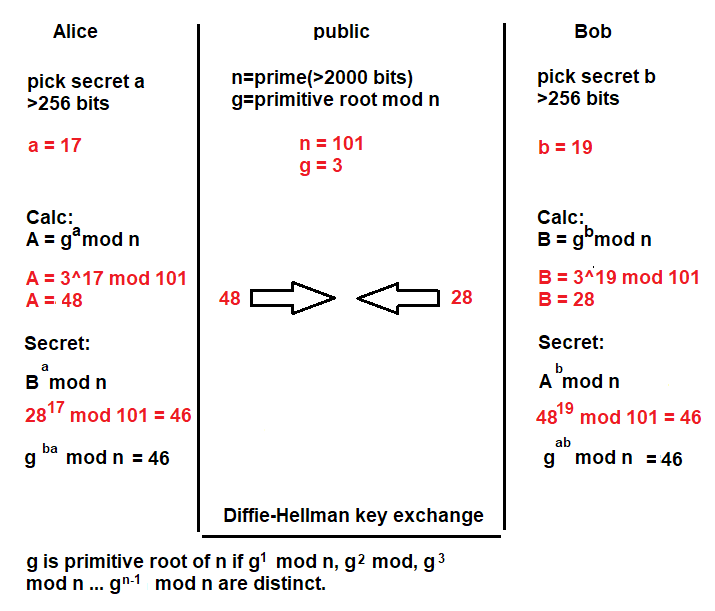 The Diffie-Hellman key exchange is a method used to securely share cryptographic keys between two parties over an insecure channel, allowing them to establish a shared secret key for encrypted communication.
The Diffie-Hellman key exchange is a method used to securely share cryptographic keys between two parties over an insecure channel, allowing them to establish a shared secret key for encrypted communication.Step 1: Alice and Bob get public numbers n = 101, g = 3
Step 2: Alice selected a private key a = 17 and
Bob selected a private key b = 19
Step 3: Alice and Bob compute public values
Alice: A =(3^17 mod 101) = 48
Bob: B = (3^19 mod 101) = 28
Step 4: Alice and Bob exchange public numbers
Step 5: Alice receives public key B =28 and
Bob receives public key A = 48
Step 6: Alice and Bob compute symmetric keys
Alice: 28^17 mod 101 = 46
Bob: 48^19 mod 101 = 46
Step 7: 46 is the shared secret.
Explanation of the RSA algorithm
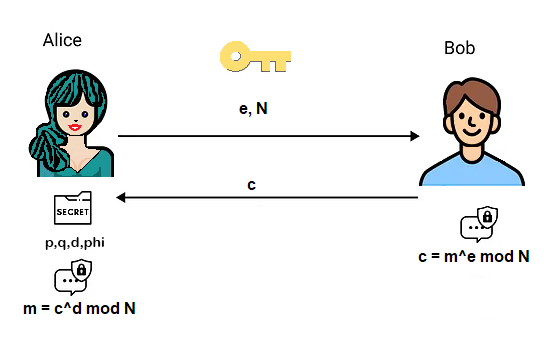 Asymmetric encryption — a message is encrypted using a public key and decrypted using a private key;
e and N are the public key for everyone to see and use, p,q and phi(n) are kept secret, d is the private key, also kept secret, m is a number representing the message, C is the encrypted message sent to Alice over an insecure channel.
Asymmetric encryption — a message is encrypted using a public key and decrypted using a private key;
e and N are the public key for everyone to see and use, p,q and phi(n) are kept secret, d is the private key, also kept secret, m is a number representing the message, C is the encrypted message sent to Alice over an insecure channel.
Non-secret encryption In 1970 James Ellis a British engineer and mathematician was working on an idea for non-secret encryption. It's based on a simple yet clever concept lock and unlock are inverse operations. Ellis never arrived at a mathematical inverse keys solution though he had an intuitive sense of how it should work. The idea is based on splitting a key into two parts an encryption key and a decryption key. The decryption key performs the inverse or undo operation which was applied by the encryption key. A mathematical solution was needed to make this work in practice. The solution was found by another British mathematician and cryptographer Clifford Cocks. Cocks needed to construct a special kind of one-way function called a trap door function. This is a function that is easy to compute in one direction yet difficult to reverse unless you have special information called the trap door. For this he turned to modular exponentiation which we introduced as clock arithmetic in the diffie-hellman key exchange as follows: Take a number raise it to some exponent divide by the modulus and output the remainder. This can be used to encrypt a message as follows: imagine Bob has a message which is converted into a number m He then multiplies his number by itself e times where e is a public exponent then he divides the result by a random number n and outputs the remainder of the division this results in some number c. This calculation is easy to perform however given only c e and n. It is much more difficult to determine which m was used because we'd have to resort to some form of trial and error so this is our one-way function that we can apply to m easy to perform but difficult to reverse. This is our mathematical lock. What about the key. The key is some piece of information that makes it easy to reverse the encryption. We need to raise c to some other exponent say d which will undo the initial operation and return the original message m. So both operations together is the same as m to the power of e all raised to the power of d which is the same as m to the power of e times d (e is the encryption d is the decryption). Therefore we need a way for alice to construct e and d which makes it difficult for anyone else to find d. This requires a second one-way function which is used for generating d and for this he looked back to Euclid. Over 2000 years ago euclid showed every number has exactly one prime factorization which we can think of as a secret key. Example 60 = 2 × 2 × 3 × 5 (the only prime factorization)! It turns out that prime factorization is a fundamentally hard problem. So factorization is what Cocks used to build the trapdoor solution. Step one: Alice randomly generated a prime number over 150 digits long, call this p then a second random prime number roughly the same size call this q. She then multiplies these two primes together to get a number n which is over 300 digits long. This multiplication step would take less than a second. Step two: Cocks needed to find a function which depends on knowing the factorization of n. For this he looked back to work done in 1760 by swiss mathematician Leonard Euler. Euler's phi function measures the breakability of a number eulerphi(n). It outputs how many integers are less than or equal to n that do not share any common factor with n. What's interesting is that calculating the phi function is hard except in one case when p is a prime number. Since prime numbers have no factors greater than 1 the phi of any prime number p is simply p minus one. The phi function is also multiplicative that is phi a times b equals phi a times phi b. If we know some number n is the product of two primes p and q then phi of n is just the value of phi for each prime multiplied together or p minus 1 times q minus 1. If you know the factorization for n then finding phi n is easy: phi=(p-1)(q-1) Step 3: How to connect the phi function to modular exponentiation? For this he turned to euler's theorem which is a relationship between the phi function and modular exponentiation as follows: m to the power of phi(n) is congruent (≡) to one (mod n). m and n need to be coprime (gcd(m,n)=1) m^phi(n) mod n = 1 // 12^60 mod 77 = 1 Now we just need to modify this equation using two simple rules. First if you raise the number 1 to any exponent k you always get one. In the same way we can multiply the exponent phi(n) by any number k and the solution is still one. m^(phi(n)*k) ≡ 1 (mod n) // 12^(60*4) mod 77 = 1 Second if you multiply one by any number, say m, it always equals m In the same way we can multiply the left side by m to get m on the right hand side and this can be simplified as m to the power of k times phi n plus one. m^k.phi(n)+1 ≡ m (mod n) // multiplied by m; on the left it results in +1 This is the breakthrough. We now have an equation for finding e times d which depends on phi(n). Therefore it's easy to calculate d only if the factorization of n is known. Meaning d should be alice's private key The private key will allow her to undo the effect of e. m^ed mod n = m // m=message e=encryption d=decryption n=p*q e*d = k.phi(n)+1 // conclusion gcd(e,phi(n))=1 //This ensures e has an inverse modulo phi(n). To find d the Extended Euclidean algorithm is used, solved in the following way: k.phi(n)+1 mod phi(n) = 1, so e*d mod phi(n) = 1 d=e^-1 mod phi(n) Example Bob has a message he converted into a number using a padding scheme. Let's call this m. Then alice generates her public and private key as follows: first she generates two random prime numbers of size > 2000 bits and multiplies them to get n, then she calculates phi of n easily since she knows the factorization of n. Next she picks some public exponent e, (65537 is a common compromise between being high, and increasing the cost of raising to the e-th power) with the condition that 1 < e < phi(n) and gcd(e,phi(n)) = 1 not sharing a factor with phi(n). Finally she finds the value of her private exponent d In GP/PARI calculator allocatemem(120000000) // stack size 114 MB) q=primes(2000)[random(2000) + 1] q= 14149 p=primes(2000)[random(2000) + 1] p= 5581 n=p*q n= 78965569 phi=eulerphi(n) phi = 78945840 e=17 // pick a number 1 < e < phi gcd(e,phi) // e is coprime with phi = 1 // true d=bezout(e,phi)[1] // extended Euclidian algorithm d = 4643873 d=e^-1 % phi // another way of calculating d d = 4643873 m=12 // m=message c=m^e % n // c=cypher c= 46606799 w=c^d % n // w=decrypted c w= 12 // w = m If n is large enough Alice can be sure that prime factorization of n will take hundreds of years even with the most powerful network of computers. This method was immediately classified after its publication however it was independently rediscovered in 1977 by Ron Rivest, Adi Shamir and Leonard Adleman its strength relies on the hardness of prime factorization.
Diana cipher wheel
 During the Vietnam War "clandestine" communication between US military forces was based on the Diana Cryptosystem. This methode to encode en decode messages
is theoretically unbreakable when used properly. The cryptographic cipher is
based on two techniques.
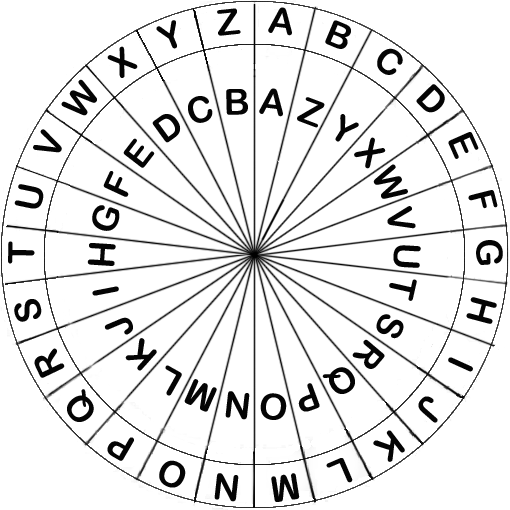
First of all, it uses a trigraph to convert two letters into a third letter.
This conversion uses a fixed lookup table — an example of which is pictured on the left — that maps each combination of two letters (blue & green into a third red letter.
What is specific about this conversion is that for each triplet of letters it
holds that any two letters of the triplet are always converted into the third
letter of the triplet. For example, if it is given that the letters B and K are
converted in the letter O, then we also know that the letters K and B yield the
letter O, and also that the letters O and B yield the letter K, and that the
letters K and B yield the letter O. Actually, it is quite easy to compute the
conversion. If we find the two given letters in the alphabet at positions and
(where A is at position 0, B is at position 1, and so on), then we find the
third letter in the alphabet at position, where the operator represents the
remainder after integer division.
During the Vietnam War "clandestine" communication between US military forces was based on the Diana Cryptosystem. This methode to encode en decode messages
is theoretically unbreakable when used properly. The cryptographic cipher is
based on two techniques.
First of all, it uses a trigraph to convert two letters into a third letter.
This conversion uses a fixed lookup table — an example of which is pictured on the left — that maps each combination of two letters (blue & green into a third red letter.
What is specific about this conversion is that for each triplet of letters it
holds that any two letters of the triplet are always converted into the third
letter of the triplet. For example, if it is given that the letters B and K are
converted in the letter O, then we also know that the letters K and B yield the
letter O, and also that the letters O and B yield the letter K, and that the
letters K and B yield the letter O. Actually, it is quite easy to compute the
conversion. If we find the two given letters in the alphabet at positions and
(where A is at position 0, B is at position 1, and so on), then we find the
third letter in the alphabet at position, where the operator represents the
remainder after integer division.
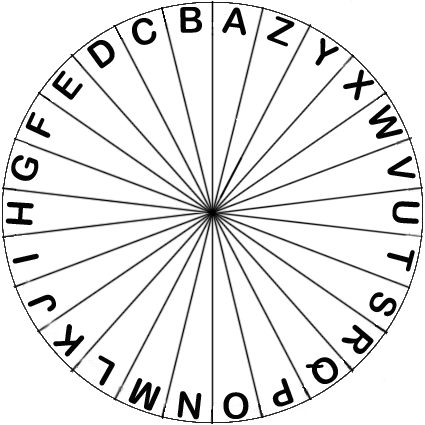 Home made Diana cipher wheel. Using wooden disks 18cm and 15cm bought from Lazada (80bht). Created two images with the alphabet, had them printed on 260gr paper. To determine the centre and drill a hole you need to be very meticulous. I used a paper template with a second and third circle of letters to find the right spot to cut the window in the second disk.
Second technique of the Diana cipher is the use of one-time pads. There were only two matching pads in existence and they would only be used one time. There were booklets that contained randomly generated groups of 5-letter words, 30
words to a page. The person sending a message would first write the letters to the message, over these random groups of
words. Included in the front of each one-time pad was a one-page encryption table. If I wanted to send the letter P,
and the letter under the P was an A, then I would send a K. The person listening on the frequency at the other end,
would have the other matching pad. They would write the letter they received (a K) over the letter in their one-time
pad (an A), and decipher it based on the table, yielding the original letter P.
Each communication site in Vietnam (we had over 100 A-Camps along the Cambodian / Laotian border, and some 20 B-detachment sites spread over the country) had a different pad, depending on the location they were having the commo-check with. It obviously was very important that both people were using the appropriate matching pads, or the deciphered messages would not make any sense.
Home made Diana cipher wheel. Using wooden disks 18cm and 15cm bought from Lazada (80bht). Created two images with the alphabet, had them printed on 260gr paper. To determine the centre and drill a hole you need to be very meticulous. I used a paper template with a second and third circle of letters to find the right spot to cut the window in the second disk.
Second technique of the Diana cipher is the use of one-time pads. There were only two matching pads in existence and they would only be used one time. There were booklets that contained randomly generated groups of 5-letter words, 30
words to a page. The person sending a message would first write the letters to the message, over these random groups of
words. Included in the front of each one-time pad was a one-page encryption table. If I wanted to send the letter P,
and the letter under the P was an A, then I would send a K. The person listening on the frequency at the other end,
would have the other matching pad. They would write the letter they received (a K) over the letter in their one-time
pad (an A), and decipher it based on the table, yielding the original letter P.
Each communication site in Vietnam (we had over 100 A-Camps along the Cambodian / Laotian border, and some 20 B-detachment sites spread over the country) had a different pad, depending on the location they were having the commo-check with. It obviously was very important that both people were using the appropriate matching pads, or the deciphered messages would not make any sense.
After a while, most of us soldiers became so proficient with the system, that they actually learned the deciphering matrix by heart. No matter what pads anyone had, the combinations always were the same. i.e. Any 3 letters always went together, regardless of the order; BKO/KOB/OBK/BOK/KBO/OKB. After listening to thousands and thousands of transmissions, it really got quite simple.
Diana cipher simulated in C.
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <ctype.h>
void usage(int nr, char *arg[]) {
for (int i=0; i < nr; i++) {
printf("%s ", arg[i]);
}
printf("%d\n", nr);
printf("\nusage: ./diana -k key -[c|m] [msg|code]\n");
exit(1);
}
int main(int argc,char *argv[]) {
unsigned char key[100]={'\0'};
unsigned char msg[100]={'\0'};;
unsigned char code[100];
unsigned char k,m;
unsigned int i,y = 0;
unsigned int keystart,keyend,keylen;
if (argc < 5) {
usage(argc,argv);
}
for (i=1; i < argc; i++) {
if (strcmp(argv[i], "-k") == 0) {
keystart = i+1;
} else if ((strcmp(argv[i], "-m") == 0) || (strcmp(argv[i], "-c") == 0)) {
keyend = i;
}
}
for (i=keystart; i < keyend; i++) {
strcat(key,argv[i]);
}
keylen=strlen(key);
for (i=keyend+1; i < argc; i++) {
strcat(msg,argv[i]);
}
for (i=0; i < strlen(msg); i++) {
if (y >= keylen) y = 0;
k = toupper(key[y]);
m = toupper(msg[i]); // k + M + C = 220 or 246
if ((220 - k - m) < 65) code[i]=246 - k - m;
else code[i] = 220 - k - m;
y++;
}
code[i]='\0';
printf("%s\n",code);
return 0;
}